By Alex Beaudin, with feedback from Sam Chepal

Introduction

Market making is a crucial aspect of open finance. Exchanges (both centralized and decentralized) rely on active market makers to provide their users with access to liquidity. If the exchange aids market makers in providing competitive prices for derivatives, this will attract users. However, market makers face the burden of latency when dealing with decentralized exchanges, which often decreases the available liquidity and makes it more expensive for users to trade onchain. In this article, we explore the tangible effects of latency on market makers’ ability to provide competitive spreads, and explore why latency is so important for facilitating healthy defi liquidity in blockchain systems.

First, let’s dive a bit deeper into the roles of market makers on exchanges, and what we mean when discussing latency.

Market Makers

Market makers are market participants who are willing to, at any time, buy from or sell to market participants. For a swap, they are willing to swap asset A for asset B (say ETH for DAI) or vice-versa. For perps, they agree to enter a short position on BTC-PERP if another trader wants to long it.

Importantly, market makers don’t offer to sell and buy at the same price, they charge a premium for being available at all times called the spread. If BTC is trading at $30k, they might only buy BTC for $29k and sell it at $31k, thus making money for taking on risk. In this case, the spread is $2k, or 6.7%.

To remain competitive with other market makers, they have to keep spreads small. If they make the spread too small, however, they risk losing money to smart market participants. Being a good market maker involves carefully balancing the spread to remain competitive and profitable, which is no easy feat.

Latency

The latency measures the time it takes for an order to make it to the exchange. Higher latency means that it takes longer for your messages to make it to whatever platform you are interacting with.

For example, if Ethereum has ~15 seconds of latency, it takes fifteen seconds from the time you send a transaction for that transaction to be registered on chain. This isn’t ideal: a lot of things can happen in fifteen seconds! Ideally, latency would be 0s and things would happen as soon as we wanted them to, but this is, unfortunately, not possible since we have to communicate over long distances, and, in the case of Ethereum, we have to come to consensus to create blocks. Nonetheless, we can strive to minimize latency and take its effects into consideration when making decisions.

We’ll take a look at the effects of latency on market making in this post.

Impact of Latency on Market Making

Let’s start with an example to start thinking about how market makers might react to latency. Say we are market-making an ETH-DAI pool, and the current price of ETH is 4000DAI / ETH. We’re feeling very generous, so we market make with no spread: anyone can buy or sell ETH for exactly 4k DAI. However, we know that it will take 1s for our liquidity to hit the exchange. By the time it does, ETH might be trading for 4001 DAI, and we’ll get arbitraged. We’re feeling generous, but we don’t want to lose everything, either.

Let’s say we’re reasonably confident that in that one second, ETH could trade as low as 3999 DAI, or as high as 4001 DAI, but probably not beyond that. Then we’ll set our liquidity to take that into account: our spread will be 2 DAI. We’ll be offering a good price, and probably won’t get arbitraged.

But how do we know how much ETH will move in 1s? What’s a good benchmark? What if the latency changes, and becomes smaller or larger than 1s? Let’s talk a bit about Brownian Motion to see how we could tackle the problem.

Geometric Brownian Motion

Let’s say we have a stock with price \(S_t\). We expect that, a small amount of time later, the stock price will change by some random factor. It might go up by 1%, or down by 1%. In the case of stocks, we have what we call a geometric Brownian motion (making BSM assumptions). \(S_t\) satisfies

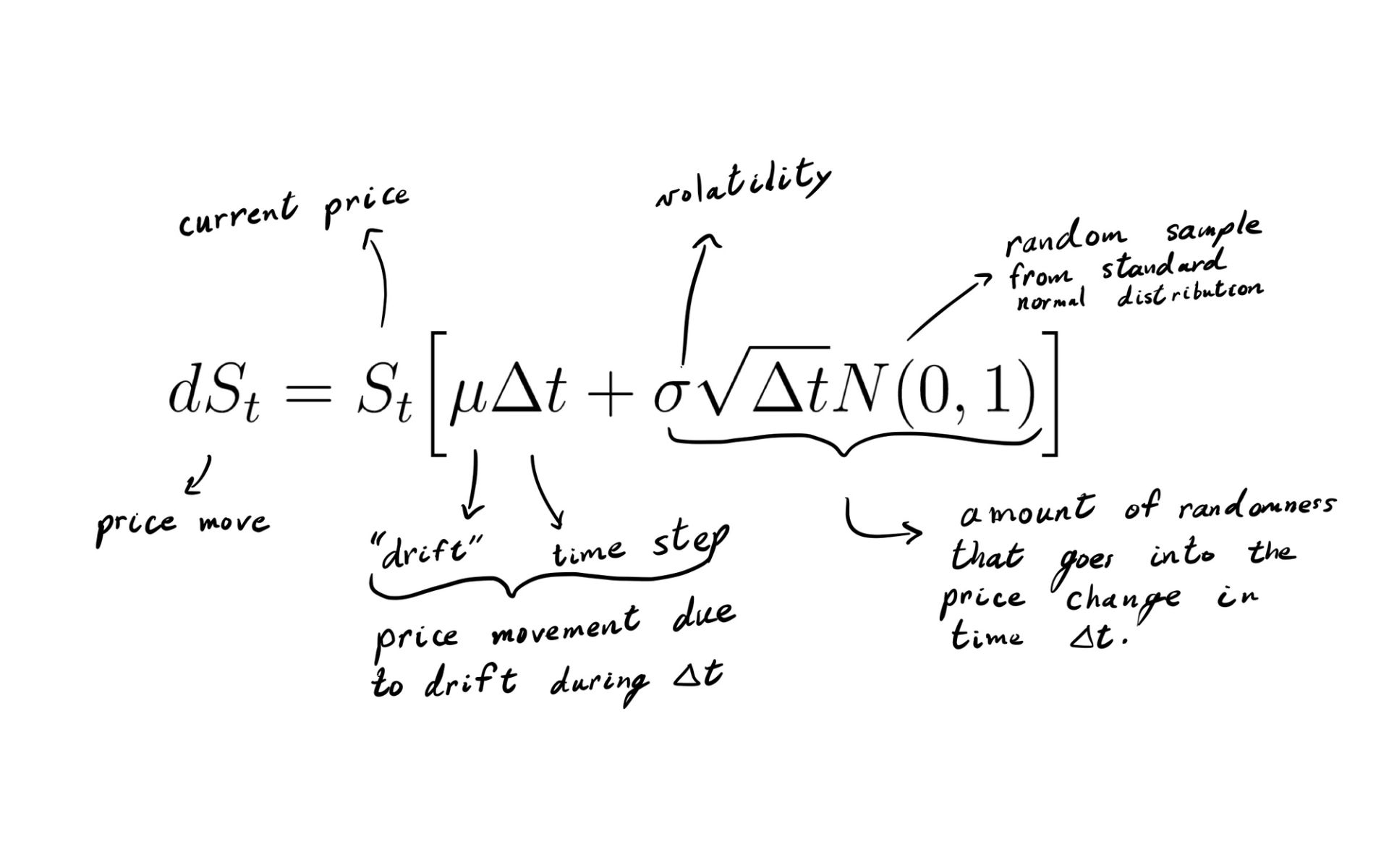
In words, the proportional change \(dS_t / S_t\) is related to a term which predicts a constant growth for each elapsed second, \(\mu \Delta t\) , and a random term, \(\sigma \sqrt{\Delta t} N(0, 1)\). Again, N(0,1) is the [standard normal distribution](https://en.wikipedia.org/wiki/Normal_distribution). (Formally, the random term is \(\sigma \sqrt{\Delta t} X\), where \(X \sim N(0, 1)\), or X is normally distributed. It is a random value sampled from the normal distribution.) Stocks typically have long-tailed distributions, i.e. not normal, but the normal distribution will suffice for our calculations.

For the sake of this post, we can consider that market makers set their prices according the current price of an asset, say ETH, at \(S_t\). By the time their orders hit the exchange, \(\Delta t\) later, the price of ETH has changed slightly to \(S_{t + \Delta t}\) and people are starting to arbitrage. How much do we expect our market maker to increase their spread to remain profitable? If they don’t, how much do they expect to net in losses over a trading day?

Well our GBM equation above tells us how much we expect the price to change!

Following our initial ETH-DAI example, this motivates us to increase our spread relative to this amount. However, we should first note a few things. Let’s assume the market makers have access to all the parameters in the equation above, including the latency. Then they can tell exactly what \(\mu \Delta t\) is. In other words, they know the price will move by some amount that is not random, and they can preemptively adjust their price to take this into account. They can’t predict the other term, though, \(\sigma \sqrt{\Delta t} N(0, 1)\), since it depends on a random sample from the normal distribution. This is the term which determines how much market makers have to increase their spread to account for price uncertainty due to latency. They don’t know if they price will move up or down, so they account for both.

The fractional spread increase, s, is given by

where \(z\) is the variable of interest for a market maker, and is related to their preferences in relation to N(0,1). Importantly, it is a constant once the market maker determines their preferences. For example, if the market maker cared about the price staying within the spread most of the time, then they would pick \(z \approx 0.66\). For this value of z, about 50% of price swings will be within their spread. For \(z = 2\), about 95% of price swings will be within the spread. See Appendix A for the more general case. Now let’s look at how this spread will affect markets at different latencies.

So how big is this?

Picking z = 1, and looking at BTC-PERP for millisecond latencies, we get (roughly)

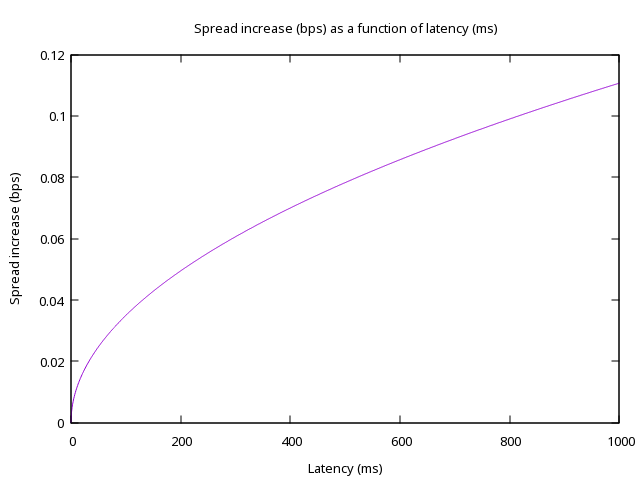
This might look like a very small effect. We only increase the spread by 0.1bps even with a whole second of latency. However, for a very competitive exchange, 0.1bps is a huge difference. Binance, for example, routinely has BTC-PERP spreads within 0.05bps — adding 0.1bps would triple the spread! Even adding just 10ms would add 0.01bps, a 10% increase. Moreover, we assumed the market maker picked z = 1, which would make them extremely generous. Let’s compare this graph to spread on current exchanges, and see how they rack up

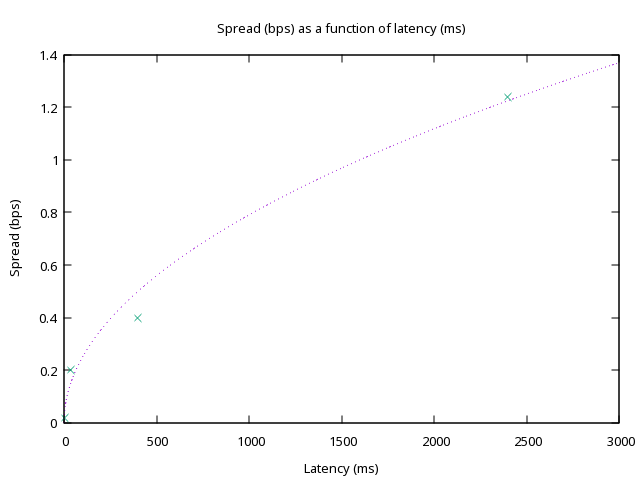
A couple of things to note. First of all, we have the right shape! Secondly, this graph should be taken with a grain of salt: spread depends on many more factors than latency. Importantly, we didn’t take into consideration the effects of competition, volume, fees, etc. Moreover, we actually had to fit the value of \(\sigma z\), since it turns out market makers are less generous than we were, and overestimated the volatility and increased z so \(\sigma z \approx 0.076 \text{bps} \cdot \text{ms}^{-1/2}\). We expected market makers to increase their spread proportionally to \(\sqrt{\Delta t}\), which is indeed what happens. The important bit is that it doesn’t matter if market makers are nice or generous or not, they cannot get around latency. If the latency increases, they have no choice but to increase spreads to the detriment of traders.

Quantifying loss

Let’s say an exchange wanted to subsidize market-making by offering incentives to offset the effects of latency on market-making spreads. How much would the exchange have to pay? Back-testing the effects of price movements on market-making strategies on BitMEX can give us an idea of how much money is lost to arbitraging. We expect the volume to be taken in that amount of time to be proportional to \(\sqrt{\Delta t}\), but also the size of orders grows further away from the index price. For higher latencies, we expect the loss to grow faster than the square root, maybe even linearly. Which is indeed what we observe.

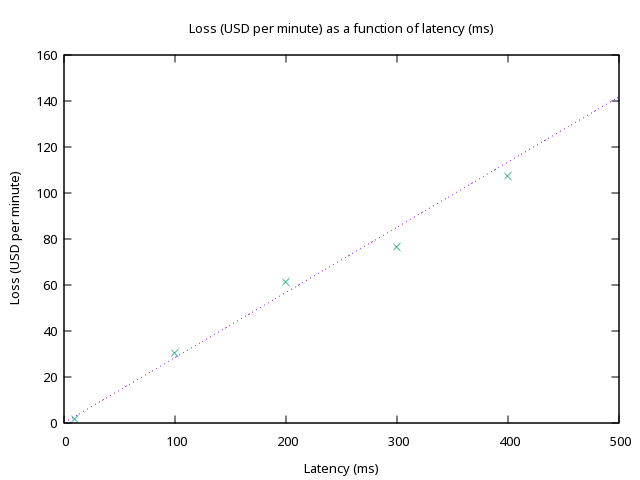
For an exchange with the latency of Solana, around 400ms, (and the order book sizes of BitMEX) we expect to pay $100 per minute. This might not sound like a lot, but it adds up to $144k a day! Suffice it to say, latency matters… a lot! If there was a decentralized or transparent exchange that could offer the security of decentralized exchanges with the latency of a centralized exchange, everyone would win.

Conclusion

Latency is of critical consideration when considering design choices for exchanges, in particular CLOBs. Maintaining low latency is critical to enabling market makers to offer competitive spreads. Unfortunately, low latencies are currently exclusive to centralized solutions. Current decentralized exchanges are limited by block time when considering latencies, making existing L1 and even L2 blockchains susceptible to high spreads regardless of market maker skill. This is a huge challenge for attracting traders, since the added latency of decentralized alternatives add an important effective fee to everyday traders. To properly compete against centralized venues, blockchains need to adopt extremely low latency solutions at least on the order of milliseconds. We're excited to be working on one such solution, Layer N's NordVM, to enable an ultra low latency blockchain system capable of real-time transaction processing.

Appendix A

General calculation of z

More generally, if the market makers want a fraction \(f\) of all swings to be within their spread, they should pick

where \(\Phi^{-1}\) is the inverse c.d.f. of N(0,1). This is what it looks like

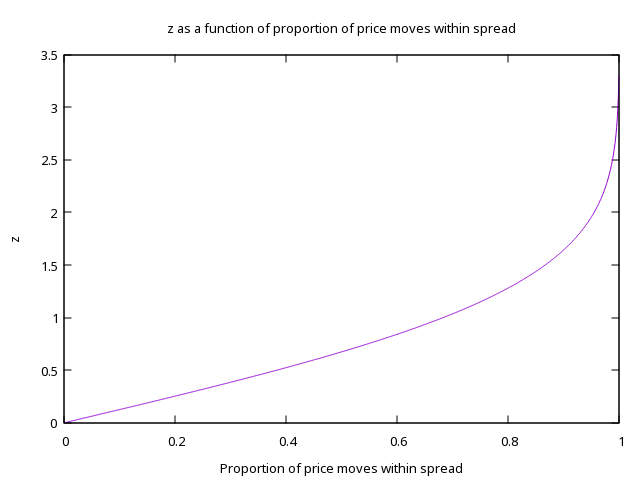
So if we wanted to capture, say, 80% of price movements within the spread, we should pick \(z \approx 1.25\).